The Economics of Instant Hot Water: Quooker vs Kettle

How long will it take for an instant hot water tap to save some money?

I recently visited my cousin Robyn in the United Kingdom. In her house there was, in addition to a standard tap in the kitchen sink, a tap that dispensed boiling water instantly. It was convenient, removing almost entirely the delay between the thought of tea and the first sip. But is it economically sound compared to a simple electric kettle?

TLDR: I calculated that it would take 147.4 years for the instant hot water tap to be more cost-effective than a kettle. This is because the instant hot water tap is much more expensive than a kettle up-front, and the energy savings are minimal even under an improbable use case of 8 cups of tea per day.

Read on to see how I came to this conclusion, and play with the assumptions in order to calculate how long it would take for the Quooker to be more cost-effective than a kettle for your family.¹

What is an instant hot water tap?

The instant hot water tap system consists of a small, pressurised reservoir that is heated to 110 degrees Celsius and a tap to dispense the water. The system can be installed below a kitchen sink to minimise the distance and potential heat loss between the tap and the reservoir. Because the reservoir is pressurised, the water is unable to boil, even at 110 degrees Celsius. When the tap is opened, the pressure is released, and the water boils instantly.

For the remainder of the blog, I will refer to this system as a Quooker, a dutch brand which produces these taps, about which I could find the most information on the internet.

Overview of instant hot water tap installation

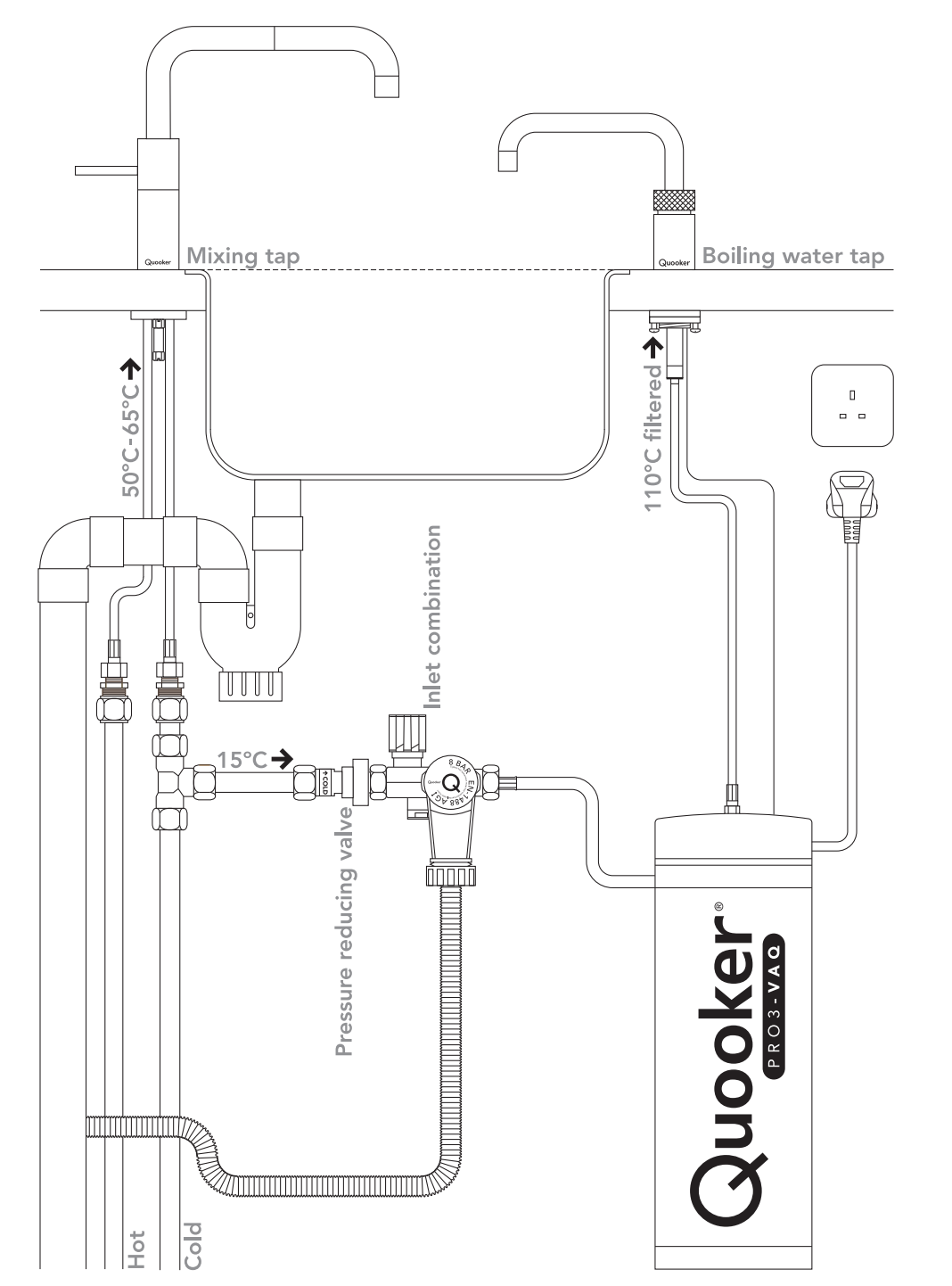
How does it compare to a kettle?

Along with convenience, the Quooker also claims to be more energy efficient than a kettle by providing the exact amount of boiling water required for a cup of tea. This is in contrast to a kettle, which is often overfilled by the user, wasting energy and water.

My goal was thus to calculate for how long these energy savings would have to accrue before the Quooker became more cost-effective than a kettle. To do this, I ask GPT-4 to help me calculate the energy consumption of both the Quooker and a standard electric kettle.

Calculating the energy consumption of the Quooker and a kettle

Assumptions

First we pin down the scenarios under which the two systems are compared. My assumptions are:

Kettle Assumptions	Quooker Assumptions	Other Assumptions
My plastic kettle is rather old, and I have no idea what its efficiency is. I assume that it is 70% efficient.	The Quooker is 90% efficient.	I drink 8 cups of tea per day.
I overfill my kettle by 250 ml.	The Quooker is always on, maintaining the water at 110 degrees Celsius and using 10 Watts to do so.	The water in the kettle cools completely between each boil.
The kettle costs € 50.	The Quooker costs € 1000.	Electricity costs € 0.3 per kWh.

Calculations

We can then calculate the energy consumption of each system. The energy consumption of the kettle is calculated as follows:

$q=mc\mathrm{\Delta }T$ where:

• q is the heat energy required (in Joules),
• m is the mass of the water (in kg),
• c is the specific heat capacity of water (4200 J/kg°C), and
• ΔT is the change in temperature (in °C).

We then convert the energy from Joules to kWh, and multiply by the electricity price to get the cost of boiling the kettle.

Energy (kWh) = Energy (Joules) / 3.6e6

Cost = Energy (kWh) * Cost per kWh

Plugging in the numbers, we get the following calculation for the energy consumption of the kettle:

Because of overfilling the kettle, we must raise the temperature of 500g of water by 80°C each time we boil the kettle, even if we only use 250g of water in our tea. The kettle requires 239.086 kilojoules of energy, or 0.07 kWh each time we boil it. This is equivalent to € 0.16 per day at 8 cups of tea per day.

For the Quooker, we get the following energy consumption:

Because the Quooker uses 10 Watts to maintain the water at 110 degrees Celsius, it uses 0.24 kWh per day in standby. This is equivalent to € 0.07 per day. In addition, we have to heat 250g of water to 110 degrees Celsius, which requires 104.6 kilojoules of energy, or 0.03 kWh for each cup of tea. This is equivalent to € 0.14 per day at 8 cups of tea per day.

So, the kettle uses € 58.18 per year, and the Quooker uses € 51.73 per year under our assumptions.

Given then price of the Quooker at € 1000 and the price of the kettle at € 50, the Quooker will pay for itself in 147.4 years.

Find out for yourself

You can adjust any of these assumptions in the inputs below to see how they affect the result. The entire article is dynamic, so adjust the inputs and read it again from the top to see how the calculations change and what the payoff period is in your case!²

import { aq, op } from '@uwdata/arquero'

  import {aq as aq, op as op} from "@uwdata/arquero"

viewof kettle_efficiency= Inputs.range(
  [50, 100], 
  {value: 70, step: 5, label: "Kettle efficiency:"}
)

viewof Quooker_efficiency= Inputs.range(
  [50, 100], 
  {value: 90, step: 5, label: "Quooker efficiency:"}
)

viewof cups_per_day= Inputs.range(
  [0, 40], 
  {value: 8, step: 1, label: "Cups of tea per day:"}
)

viewof kettle_overfill= Inputs.range(
  [0, 1000], 
  {value: 250, step: 50, label: "ml by which kettle is overfilled:"}
)

viewof Quooker_price= Inputs.range(
  [50, 2000], 
  {value: 1000, step: 50, label: "Price of Quooker (Euro):"}
)

viewof kettle_price= Inputs.range(
  [50, 2000], 
  {value: 50, step: 50, label: "Price of kettle (Euro):"}
)

viewof electricity_price= Inputs.range(
  [0, 1], 
  {value: .3, step: 0.05, label: "Price of electricity per kWh (Euro):"}
)

Kettle efficiency:

kettle_efficiency = 70

Quooker efficiency:

Quooker_efficiency = 90

Cups of tea per day:

cups_per_day = 8

ml by which kettle is overfilled:

kettle_overfill = 250

Price of Quooker (Euro):

Quooker_price = 1000

Price of kettle (Euro):

kettle_price = 50

Price of electricity per kWh (Euro):

electricity_price = 0.3

c = 4.184  // Specific heat capacity of water in J/g°C
T_change = 80  // Change in temperature for kettle (100°C - 20°C)
T_change_Quooker = 90  // Change in temperature for Quooker (110°C - 20°C)
water_density = 1  // Density of water in g/mL
mass_tea = 250 * water_density
mass_overfill = kettle_overfill * water_density
mass_kettle = mass_tea + mass_overfill
Q_kettle = (mass_kettle * c * T_change) / (kettle_efficiency / 100)  // Energy in joules
Q_kettle_kWh = Q_kettle / (3.6 * Math.pow(10, 6))  // Convert energy to kWh
total_kettle_energy = Q_kettle_kWh * cups_per_day // Total energy for kettle per day
Q_Quooker = (mass_tea * c * T_change_Quooker) / (Quooker_efficiency / 100)  // Energy in joules
Q_Quooker_kWh = Q_Quooker / (3.6 * Math.pow(10, 6))  // Convert energy to kWh
total_Quooker_energy = (Q_Quooker_kWh * cups_per_day) + 0.24  // Total energy for Quooker per day
kettle_cost_daily = total_kettle_energy * electricity_price
Quooker_cost_daily = total_Quooker_energy * electricity_price
kettle_cost_yearly = kettle_cost_daily * 365
Quooker_cost_yearly = Quooker_cost_daily * 365

kettle_cost_yearly_round = Math.round(kettle_cost_yearly * 100) / 100
Quooker_cost_yearly_round = Math.round(Quooker_cost_yearly * 100) / 100

Q_kettle_wasted = (mass_overfill * c * T_change) / (kettle_efficiency / 100)
Q_kettle_wasted_kWh = Q_kettle_wasted / (3.6 * Math.pow(10, 6))
total_kettle_energy_wasted = Q_kettle_wasted_kWh * cups_per_day
total_kettle_energy_wasted_round = Math.round(total_kettle_energy_wasted * 100) / 100
total_kettle_energy_wasted_cost_round = Math.round(total_kettle_energy_wasted * electricity_price * 365)
percentage_kettle_energy_wasted = Math.round(total_kettle_energy_wasted / total_kettle_energy * 100)

Q_Quooker_wasted = 0.24
total_Quooker_energy_wasted_cost_round = Math.round(Q_Quooker_wasted * electricity_price * 365)
percentage_Quooker_energy_wasted_round = Math.round(Q_Quooker_wasted / total_Quooker_energy * 100)

years = (Quooker_price - kettle_price) / (kettle_cost_yearly - Quooker_cost_yearly)
years_round = Math.round(years * 100) / 100

c = 4.184

T_change = 80

T_change_Quooker = 90

water_density = 1

mass_tea = 250

mass_overfill = 250

mass_kettle = 500

Q_kettle = 239085.7142857143

Q_kettle_kWh = 0.06641269841269841

total_kettle_energy = 0.5313015873015873

Q_Quooker = 104600

Q_Quooker_kWh = 0.029055555555555557

total_Quooker_energy = 0.47244444444444444

kettle_cost_daily = 0.15939047619047617

Quooker_cost_daily = 0.14173333333333332

kettle_cost_yearly = 58.1775238095238

Quooker_cost_yearly = 51.73266666666666

kettle_cost_yearly_round = 58.18

Quooker_cost_yearly_round = 51.73

Q_kettle_wasted = 119542.85714285714

Q_kettle_wasted_kWh = 0.033206349206349205

total_kettle_energy_wasted = 0.26565079365079364

total_kettle_energy_wasted_round = 0.27

total_kettle_energy_wasted_cost_round = 29

percentage_kettle_energy_wasted = 50

Q_Quooker_wasted = 0.24

total_Quooker_energy_wasted_cost_round = 26

percentage_Quooker_energy_wasted_round = 51

years = 147.4043534157912

years_round = 147.4

dt = aq.table({
  years: Array.from({length: 200}, (_, i) => i + 1),
  kettle: Array.from({length: 200}, (_, i) => {
    return (i + 1) * kettle_cost_yearly + kettle_price
  }),
  Quooker: Array.from({length: 200}, (_, i) => {
    return (i + 1) * Quooker_cost_yearly + Quooker_price
  })
})

// Prepare the data in a format suitable for Plot.line
data = dt.objects().flatMap(({years, kettle, Quooker}) => [
  {years, value: kettle, key: 'Kettle'},
  {years, value: Quooker, key: 'Quooker'}
]);

Plot.plot({
  y: {
    grid: true,
    label: 'Cumulative cost (Euro)'
  },
  x: {
    grid: true,
    label: 'Time (years)'
  },
  color: {
    domain: ["Kettle", "Quooker"], legend: true, type: "categorical", range: ["#1f77b4", "#ff7f0e"]
  },
  marks: [
    Plot.line(data, {x: 'years', y: 'value', stroke: 'key'})
  ]})

dt = Table: 3 cols x 200 rows {_names: Array(3), _data: Object, _total: 200, _nrows: 200, _mask: null, _group: null, _order: null, _params: undefined, _index: null, _partitions: null}

data = Array(400) [Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, Object, …]

KettleQuooker

How much energy is lost by each system?

Waste Calculation	Kettle	Quooker
Reason for waste	Due to overfilling	Due to heat loss
kWh wasted per day	0.27 kWh	0.24 kWh
Percentage of total energy	50%	51%
Cost of waste per year	€ 29	€ 26

What else do we learn?

As the number of cups of tea increases, the Quooker becomes more cost-effective than the kettle, as the wasted energy is a fixed amount, while the wasted energy of the kettle increases linearly with the number of cups of tea, assuming the overfilling remains constant.

Reducing the amount by which we overfill the kettle decreases the energy loss and the cost of operating the kettle.

Appendix

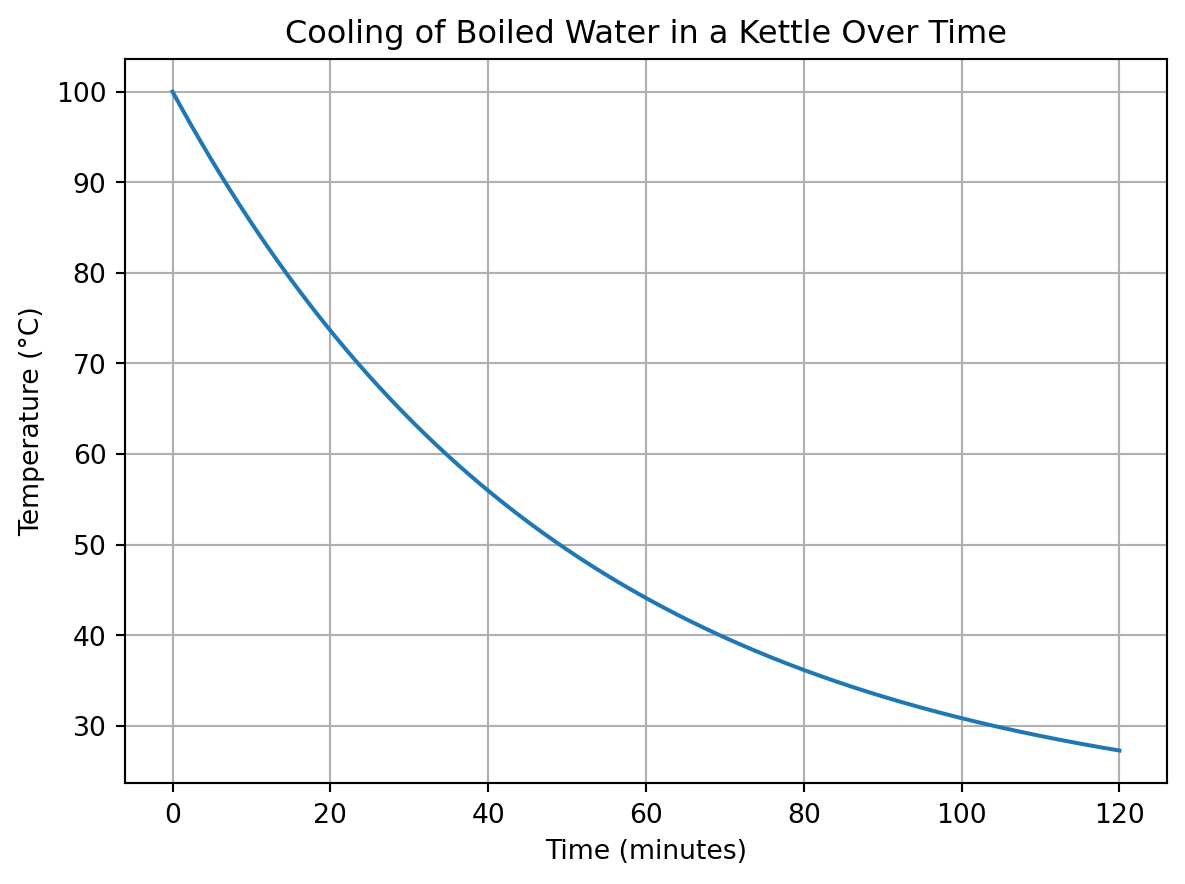
I have assumed that the water in the kettle cools completely between each boil. This would require 2 hours between each boil, assuming an ambient temperature of 20 degrees Celsius and a cooling constant of 0.02. The cooling constant would change based on the specific kettle/environment. See the code below for the simulation.

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint

# Define the function to compute derivative
def model(T, t):
    T_ambient = 20  # Ambient temperature in degree Celsius
    k = 0.02  # Cooling constant. This would change based on the specific kettle/environment
    dTdt = -k * (T - T_ambient)
    return dTdt

T0 = 100  # Starting temperature of the water in degree Celsius

t = np.linspace(0, 120, num=500)  # Time points in minutes. Here we simulate for 2 hours

# Solve the ODE
T = odeint(model, T0, t)

# Plot the results
plt.plot(t, T)
plt.xlabel('Time (minutes)')
plt.ylabel('Temperature (°C)')
plt.title('Cooling of Boiled Water in a Kettle Over Time')
plt.grid(True)
plt.show()

Footnotes

1. The article is dynamic, so adjust the inputs and read it again from the top to see what the payoff period is in your case!

2. If for instance, you drink 25 cups of tea per day, the Quooker will pay for itself in 12.5 years.